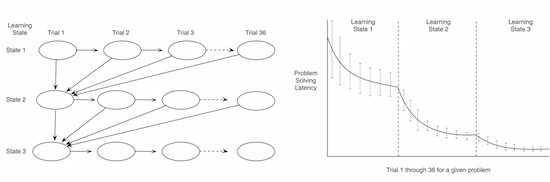
A focus of early mathematics education is to build fluency through practice. Several models of skill acquisition have sought to explain the increase in fluency due to practice by modeling both the learning mechanisms driving this speedup and the changes in cognitive processes involved in executing the skill (such as transitioning from calculation to retrieval). In the current study, we use hidden Markov modeling to identify transitions in the learning process. This method accounts for the gradual speedup in problem solving and also uncovers abrupt changes in reaction time, which reflect changes in the cognitive processes that participants are using to solve math problems. We find that as participants practice solving math problems they transition through three distinct learning states. Each learning state shows some speedup with practice, but the major speedups are produced by transitions between learning states. In examining and comparing the behavioral and neurological profiles of each of these states, we find parallels with the three phases of skill acquisition proposed by Fitts and Posner (1967): a cognitive, an associative, and an autonomous phase.

Tenison, C., & Anderson, J. (2015). Modeling the distinct phases of skill acquisition. Journal of Experimental Psychology: Learning, Memory, and Cognition .(Paper available here) (Author prepublication available here)