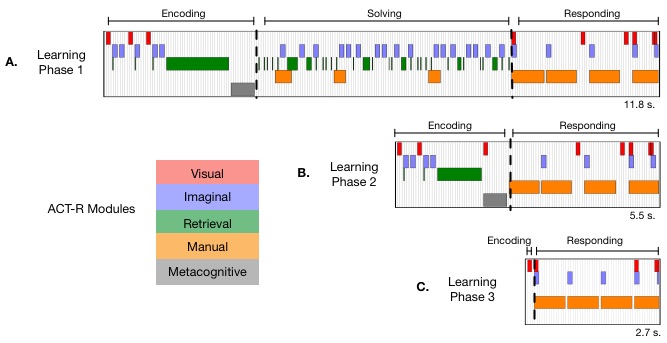
This fMRI study examines the changes in participants' information processing as they repeatedly solve the same mathematical problem. We show that the majority of practice-related speedup is produced by discrete changes in cognitive processing. Because the points at which these changes take place vary from problem to problem, and the underlying information processing steps vary in duration, the existence of such discrete changes can be hard to detect. Using two converging approaches, we establish the existence of three learning phases. When solving a problem in one of these learning phases, participants can go through three cognitive stages: Encoding, Solving, and Responding.Each cognitive stage is associated with a unique brain signature. Using a bottom-up approach combining multi-voxel pattern analysis and hidden semi-Markov modeling, we identify the duration of that stage on any particular trial from participants brain activation patterns. For our top-down approach we developed an ACT-R model of these cognitive stages and simulated how they change over the course of learning. The Solving stage of the first learning phase is long and involves a sequence of arithmetic computations. Participants transition to the second learning phase when they can retrieve the answer, thereby drastically reducing the duration of the Solving stage. With continued practice, participants then transition to the third learning phase when they recognize the problem as a single unit and produce the answer as an automatic response. The duration of this third learning phase is dominated by the Responding stage.

Tenison, C., Fincham, J. & Anderson, J. (In Press). Phases of learning: How skill acquisition impacts cognitive processing. (Author prepublication)

Tenison, C., & Anderson, J. (2015, May). Exploring skill acquisition with cognitive and brain-based models. Preliminary results presented at the eight annual Inter-Science of Learning Center Student and Post-Doc Conference, San Diego, CA.